Ornamentation-A
Building double curved structures with flat elements
In the last few years, the discretization of freeform surfaces has
been a topic of great interest in the field of geometrizing
architectural design, representing the first step in the creation of
buildable free forms in architecture. This method presents a new
approach to panelizing free-form surfaces, with the goal of generating
panels according to specific aesthetic criteria. Our
method is based on the application of tangent planes and their
intersection on an arbitrary double-curved surface. The novel
process in this work is that we take the surface curvature at local
points into account. This solves former problems which occurred
when intersecting the planes. The fact that there is an infinite
number of possibilities when selecting tangent planes on a surface
raises the issue of the way and conditions which make it
possible to select specific tangent planes whose intersection
would produce a desired 3D ornamental shape deduced from a
2D ornament.

surface with positive Gaussian curvature
.
.

regular pattern
.
.

„irregular“ pattern
.
.

surface with negative Gaussian curvature
.
.

regular „butterfly“ pattern
.
.

surface with negative and positive Gaussian curvature
.
.

we like this picture
.
.

problem – parabolical points
.
.

2D ornament
.
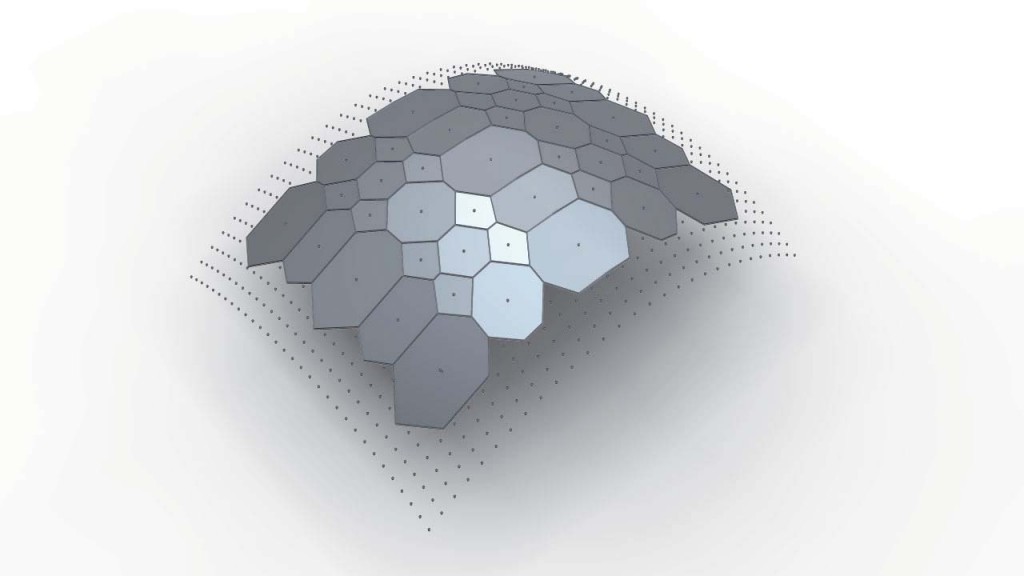
spatializing of 2D ornament
.

thickening the flat panels